카이제곱에 대한 설명에 들어가기 앞서,
자유도에 대해 먼저 간략히 설명해 보겠다.
자유도 Degree of Freedom
자유도는 주어진 통계 모델에서 독립적으로 변동할 수 있는 변수의 개수다.
이는 역설적으로 통계 모델에서 오는 제약조건이 있기 때문에 사용하는 개념이다.
다시 말해, 자유도란 모델 내에서 제약 조건에서 자유롭게 변화할 수 있는 정보의 양을 나타낸다.
예를 들어, 확률 변수 , 에 대해서,

보통 자유도는 관찰 (혹은 정보)의 수에서 추정된 매개변수의 수를 뺀 것과 같다.
일표본 T 검정
일표본 T 검정의 경우 평균 추정이라는 제약조건이 있다.
이 때, n개의 데이터의 총합은 " n * 데이터의 평균 " 이 된다는 제약이 그것이다.
예를들어, 총 10개의 데이터가 3.5의 평균을 가진다면, 데이터의 총합은 3.5 * 10, 즉 35가 된다.
10개의 데이터의 총합이 35가 되는 가지의 수는 무한하지만,
9번 째 데이터가 정해지는 순간, 10번 째 데이터도 정해진다.
그러므로, 일표본 T 검정은 10 - 1 = 9 가지의 자유로운 데이터 변환이 가능하고,
이를 n-1의 자유도를 가진다고 한다.
카이제곱 독립성 검정
카이제곱 독립성 검정의 경우, 두 가지 범주형 변수가 종속적인지 파악하는 데 상용된다.
이 때의 자유도는 각 범주의 수준 (행과 열로 표현되는)의 수에 영향을 받는다.
예를들어 2가지 범주의 2X2 수준 표를 보면 다음과 같다.

이 때, 행과 열의 총합이 정해져 있으니, 달라질 수 있는 셀 값은 단 하나다.
그러므로 이 때의 자유도는 1이다.

또한, 위처럼 3X2의 표를 보면 위와 같이 2개의 셀 값만 달라질 수 있기에, 자유도는 2다.
카이제곱 독립성 검정의 자유도는 이렇듯 하나의 공식을 따르는데,
자유도는 행이 r개, 열이 c개 있을 때 ( r - 1 )( c - 1 )이 된다.
회귀 분석
보통 자유도는 관찰 (혹은 정보)의 수에서 추정된 매개변수의 수를 뺀 것과 같다.
회귀를 수행할 때 모든 항에 대해 모수가 추정 되며, 이 때 각 항 마다 자유도를 소비한다.
카이제곱 분포
카이제곱 분포는 주로 분산 추정, 독립성 검정, 적합도 검정 등에서 활용된다.
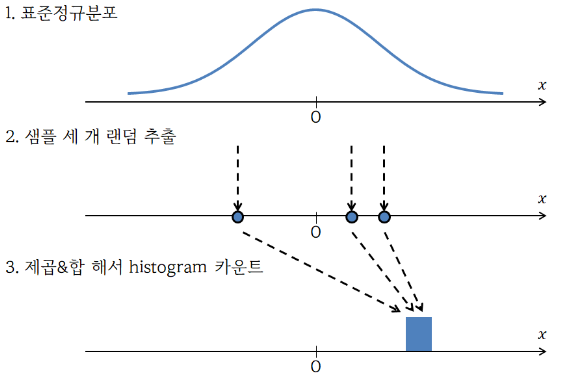
정규분포를 따르는 독립적인 확률 변수 X들에 대해,
X를 몇개 씩 추출해, 이를 제곱해 합산한 값을 카이제곱 통계량이라 한다.

이 때, 확률 변수 X를 몇개씩 뽑아 제곱합을 구하는지를 k (자유도)로 나타낼 수 있다.
k = 1인 상황은 정규분포에서 확률 변수를 1개씩만 뽑아 제곱하는 상황이고,

이를 무한히 반복해 히스토그램을 그리면 다음과 같아진다.
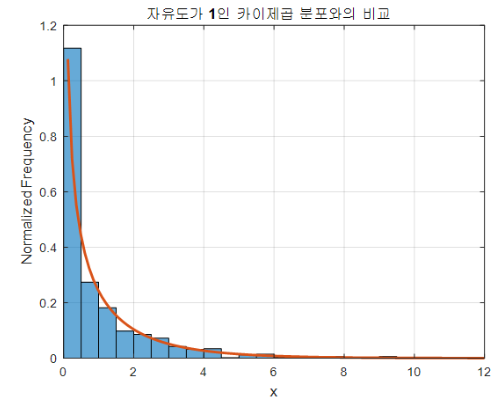
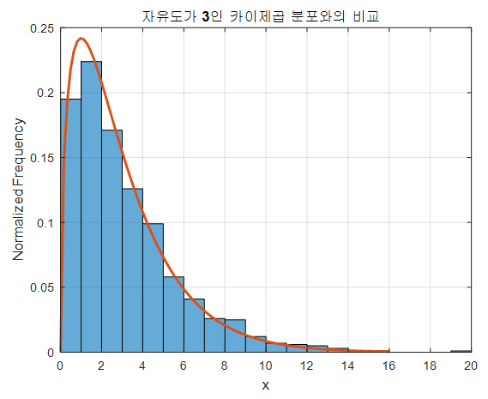
k = 3인 상황은 정규분포에서 확률 변수를 3개씩 뽑아 제곱해 서로 더하는 상황이된다.
이 또한, 무한히 반복하면 아래와 같아진다.
이 때, 카이제곱 통계량은 아래와 같은 수식으로 구할 수 있다.
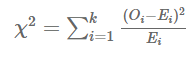
해당 식은 피어슨 카이제곱 통계량 (Pearson's chi-squared statistics) 라고도 불린다.
이 때, Oi는 i번 째 데이터에 대한 관찰값 (관측빈도), Ei는 i번째 데이터에 대한 기댓값 (기대빈도)이다.
이 때, 각 변수의 범주의 개수가 각각 k1, k2 라면,
통계량은 자유도가 (k1 - 1)(k2 - 2)인 카이제곱 분포를 따르게 된다.
예를 들어, 당뇨와 비만의 상관관계를 볼 때, 아래와 같은 2X2 테이블이 그려질 수 있다.
| 당뇨 | 정상 | 합계 | |
| 비만 체중 | ? | 20 | |
| 정상 체중 | 80 | ||
| 합계 | 25 | 75 | 100 |
당뇨 컬럼수 - 1 = 1, 비만 로우수 - 1 = 1 이므로 1 x 1로 자유도는 1이 된다.
카이제곱 검정
카이제곱 검정은 관찰되는 값과 기대값 간의 차이를 비교해 두 변수의 독립성 또는 적합도를 평가하는 데 사용된다.
기본적으로 위에서 설명한 교차분석표의 형태로 분석이 진행된다.
파이썬으로는 pandas.crosstab을 통해 교차분석표를 쉽게 만들 수 있다.
import pandas as pd
# 데이터 예시
data = {
'Gender': ['Male', 'Female', 'Female', 'Male', 'Female', 'Male', 'Female', 'Female'],
'Preference': ['Yes', 'No', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes']
}
df = pd.DataFrame(data)
# 교차분석표 (contingency table) 생성
contingency_table = pd.crosstab(df['Gender'], df['Preference'])
print(contingency_table)
[output]
Preference No Yes
Gender
Female 3 2
Male 0 3
1) 독립성 검정 Test of Independence
내가 설정한 독립변수 (원인)가 종속변수(결과)에 정말 영향을 미치는지 아니면 독립적인지를 확인하기 위한 검정이다.
즉, 인과관계를 파악하는 검정이라 할 수 있다.
이 때의 귀무가설 H0는
"독립변수는 종속변수와 상호 독립적이다." 이고,
대립가설 H1은
"독립변수는 종속변수와 독립적이지 않다, 즉 독립변수는 종속변수의 원인이 된다."가 된다.
이 때, 검정 변수의 척도는 명목 척도여야 한다.
명목 척도란 숫자의 크기에 의미가 없이 종류가 다름을 구분하는 척도로, 범주형 자료에 해당한다.
하지만 얼마나 관계가 있는지, 그 정도는 알 수 없다.
이를 파이썬을 활용하면 아래와 같이 할 수 있다.
import pandas as pd
from scipy.stats import chi2_contingency
# 데이터 예시
data = {
'Gender': ['Male', 'Female', 'Female', 'Male', 'Female', 'Male', 'Female', 'Female'],
'Preference': ['Yes', 'No', 'Yes', 'Yes', 'No', 'Yes', 'No', 'Yes']
}
df = pd.DataFrame(data)
# 교차분석표 생성
contingency_table = pd.crosstab(df['Gender'], df['Preference'])
# 카이제곱 독립성 검정 수행
chi2, p, dof, expected = chi2_contingency(contingency_table)
print(f"Chi2 Statistic: {chi2}")
print(f"P-value: {p}")
print(f"Degrees of Freedom: {dof}")
print("Expected Frequencies:")
print(expected)
[output]
Chi2 Statistic: 0.888888888888889
P-value: 0.34577858615116
Degrees of Freedom: 1
Expected Frequencies:
[[1.875 3.125] [1.125 1.875]]
위는 성별과 선호도가 독립적인지 확인하는 독립성 검정으로,
p값이 0.05보다 높으므로 "두 범주는 독립적이다."라고 할 수 있다.
2) 적합성 검정 Goodness of Fit Test
범주형 변수의 관찰 빈도가 기대빈도와 얼마나 잘 일치하는지를 검정하는 것.
기대빈도는 일반적으로 이론적 분포, 즉 정규분포 혹은 균등분포 등에 기반한다.
예를들어 주사위를 100번 던졌을 때, 각 숫자가 진짜 동일한 빈도로 나오는지를 보는것으로,
실제 1이 나온 관측빈도와 1이 나올 기대빈도인 1/6 을 비교한다.
혹은, 공을 뽑는 빈도를 통해 주머니 속에 5가지의 공이 3개씩, 총 15개가 있는지를 확인해 볼 수도 있다.
즉, 빨간 공을 뽑은 관측빈도 4개와 기대빈도 5/15 를 비교하는 것.
이 때, 귀무가설 H0인
"관찰 빈도가 기대 빈도와 일치한다." 를 기각할지를 검정하면 된다.
이를 파이썬을 활용하면 아래와 같이 사용할 수 있다.
from scipy.stats import chisquare
# 관찰된 데이터 (예: 주사위의 각 면이 나온 횟수)
observed = [18, 17, 16, 15, 17, 17] # 총 100번 던짐
# 기대되는 빈도 (균등한 분포, 즉 각 면이 동일한 확률로 나오는 경우)
expected = [100/6] * 6 # 각 면이 1/6 확률로 나오는 경우
# 카이제곱 적합성 검정 수행
chi2_statistic, p_value = chisquare(f_obs=observed, f_exp=expected)
print(f"Chi2 Statistic: {chi2_statistic}")
print(f"P-value: {p_value}")
[output]
Chi2 Statistic: 0.31999999999999995
P-value: 0.9972499265728652
위는 총 100번 관측된 각 주사위의 면수가 실제로 서로 1/6을 따르는지에 대한 적합성 검정으로,
p값이 0.05보다 높으므로 "기대빈도와 관측빈도가 일치한다." 라는 H0을 체택한다.
즉, 관측된 값을 바탕으로 주사위를 던져 각 면이 나올 확률은 1/6을 따른다.
3) 동질성 검정 Test for Homogeneity
동질성 검정은 동일한 모집단에서 나온건지 확인하는 것.
사실상 가설을 어떻게 세우느냐가 다른 것이지, 독립성 검정과 같다고 할 수 있다.
동립성은 무작위로 추출해서 둘의 응답을 보는 것.
독질성 검정은 조금 더 실험적인 상황이고, 그래서 그룹 당 몇 씩 샘플을 추출 한다.
'Statistics' 카테고리의 다른 글
| [STAT 101] ANOVA 검정과 다중 검정의 문제 (0) | 2024.08.13 |
|---|---|
| [STAT 101] T 검정과 BEST검정 (0) | 2024.08.13 |
| [STAT 101] 베이지안 AB Test의 전환율 검정과 기대수익 분석 (4) | 2024.08.13 |
| [STAT 101] 베르누이 분포와 이항 분포, 그리고 포아송 분포 (0) | 2024.08.12 |
| [STAT 101] 정규분포(Normal Distribution)와 t분포(Student's t-distribution) (0) | 2024.08.09 |