베르누이 시행 Bernoulli Trial
결과가 두 가지 중 하나로만 나오는 실험이나 시행을 베르누이 시행이라고 한다.
예시로, 동전을 던져 앞면, 뒷면이 나오게 하는 것이 베르누이 시행이다.
베르누이 확률 변수 Bernoulli Random Variable
이는 베르누이 시행의 결과를 0과 1로 표시한 것으로, 이산 확률 변수 (Discrete Random Variable)이다.

베르누이 확률 분포 Bernoulli Probability Distribution
베르누이 확률 변수의 분포를 일컫는 말로,
확률 변수 X가 베르누이 분포에 의해 발생한다면
1이 나올 확률 및 기대값을 p = Mu,
0이 나올 확률을 q = ( 1 - Mu )라 하고,
이 때 분산은 pq = Mu( 1 - Mu )가 된다.


베르누이 분포 파이썬으로 활용하기
이를 파이썬으로 활용하나면 다음과 같다
import scipy.stats as stats
mu = 0.6 # 1이 일어날 확률
rv = stats.bernoulli(mu)
type(rv)
이 때, 확률 질량 함수 Probability Mass Function은 다음과 같이 그릴 수 있다.
xx = [0, 1]
plt.bar(xx, rv.pmf(xx))
plt.xlim(-1, 2)
plt.ylim(0, 1)
plt.xticks([0, 1], ["x=0", "x=1"])
plt.xlabel("표본값")
plt.ylabel("P(x)")
plt.title("베르누이 확률변수의 확률질량함수")
plt.show()
이항 분포 Binomial Distribution
베르누이 시행을 여러 번 한다면?
성공확률이 Mu인 베르누이 시행을 N번 했을 때, 성공한 횟수를 확률변수 X라고 한다면,
X의 값은 0부터 N까지의 정수중 하나가 될 것이다.
이를 이항분포를 따르는 확률변수라고 한다.

베르누이분포와 이항분포 모두 베르누이 확률변수에서 나온 표본값이며,
베르누이 분포와 다른 점은 표본 데이터가 하나 뿐이면 베르누이분포가 되고,
표본 데이터가 여럿이면 이항분포가 된다.
이항 분포 파이썬으로 활용하기
이를 파이썬으로 활용해보면 다음과 같다.
import scipy.stats as stats
N = 10
mu = 0.6
rv = stats.binom(N, mu)
이 때, 확률 질량 함수 Probability Mass Function은 다음과 같이 그릴 수 있다.
xx = np.arange(N + 1)
plt.bar(xx, rv.pmf(xx), align="center")
plt.xlabel("표본값")
plt.ylabel("$P(x)$")
plt.title("이항분포의 확률질량함수")
plt.show()

포아송 분포 Poisson Distribution
포아송 분포는 이산확률분포에서 이항분포 다음으로 많이 사용되는 분포이다.
단위시간이나 단위공간에서 무작위로 발생하는 사건의 발생 횟수에 적용되는 분포로,
시행횟수 n이 크고, 사건의 발생 (성공)확률인 p가 매우 작은 경우에 사용한다.

이 때, 람다는 정해진 시간 안에 어떤 사건이 일어날 횟수에 대한 기대값이고,
그 사건이 n번 일어날 확률은 아래와 같다.

그러므로 포아송 분포는
평균과 분산이 람다로 같고,
1. 동일한 시간/공간 구간에서 발생할 확률이 동일하다.
2. 각 사건이 일어날 확률은 서로 독립적이다.
파이썬을 활용해 포아송 분포 그리기
이를 파이썬으로 활용해보면 다음과 같다.
from scipy.stats as stats
from numpy import arange
l = 20 # 람다 값
x = arange(41) # 41가지의 n값들
y = stats.poisson(l).pmf(x)
print(y)
이 때, 확률 질량 함수 Probability Mass Function은 다음과 같이 그릴 수 있다.
plt.figure(figsize=(12, 8))
plt.plot(x, y1, 'ro--')
plt.xlabel('X')
plt.ylabel('P(X)')
plt.title(r'$Poisson Distribution(\lambda = 20)$')
plt.grid()
plt.show()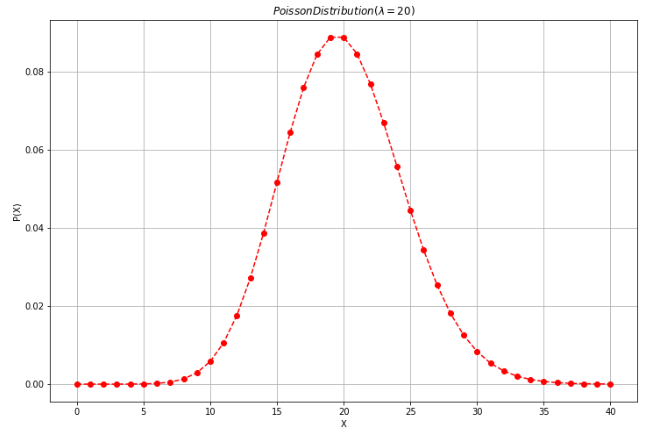
'Statistics' 카테고리의 다른 글
| [STAT 101] T 검정과 BEST검정 (0) | 2024.08.13 |
|---|---|
| [STAT 101] 베이지안 AB Test의 전환율 검정과 기대수익 분석 (4) | 2024.08.13 |
| [STAT 101] 정규분포(Normal Distribution)와 t분포(Student's t-distribution) (0) | 2024.08.09 |
| [STAT 101] 모집단과 표본, 그 속 통계 값들과 표본 추출 방법 (0) | 2024.08.07 |
| [STAT 101] 잔차와 오차, 그리고 결정계수 (0) | 2024.07.16 |