기존의 T 검정
https://thebuck104.tistory.com/34
[STAT 101] T - Test
T-test 두 그룹의 평균을 비교할 때 - student's T-test ㄴ 두 개 이상은 ANOVA test를 활용 – Analysis of Variance test ㄴ 평균의 차이 유무를 보는 것
thebuck104.tistory.com
모집단의 분산이나 표준편차를 알지 못할 때,
표본 n이 30 이하인 비교적 적은 수의 표본에 대해
모집단을 대표하는 표본으로부터 추정된 분산이나 표준편차를 가지고 검정하는 방법.
"두 모집단 의 평균 간에 차이가 없다."
라는 귀무가설과
"두 모집단의 평균 간에 차이가 있다."
라는 대립가설중 하나를 선택하도록 하는 통계적 검정 방법이다.
T 값 T-Value
T 검정에 이용되는검정통계량으로,
두 집단의 차이의 평균을 표준오차로 나눈 값이다.
즉, 표준오차와 표본평균사이의 차이의 비율을 뜻한다.

T 분포 T Distribution

평균이 0이며, 좌우 대칭을 이루는 자유도 n-1에 의해 규정되는 분포이다.
T 값이 커질 수록 표준정규분포와 같은 형태를 한다.

유의수준 알파와 자유도 df에 따른 T 값은 위와 같다.
기각역 Critical Region
귀무 가설이 기각되기 위한 검정통계랑 T 값이 위치한 범위로, 유의 수준과 자유도에 의해 결정된다.

양측검정 (Two-tailed T Test)의 경우 위와 같은 그래프의 그림을 토대로 귀무가설을 기각할지를 정하게 된다.
이 경우, 기각역이 양쪽에 존재하게 되며,

단측검정 (One-tailed T Test)의 경우에는 위와 같이 기각역이 양 끝 중 하나에 존재하게 된다.
귀무가설 Null Hypothesis
단순히 말하면 바라지 않는 가설로, 분석가가 원하는 가설을 대립가설 (Alternative Hypothesis)로 한다.
대표적으로 아래와 같이 가설을 준비할 수 있다.
- 귀무가설(H0) : 두 집단 간의 평균 차이는 없을 것이다.
- 대립가설(H1) : 두 집단 간의 평균 차이가 있을 것이다.
예컨대, 평균의 차이가 있을 가능성이 있어,
t 값이 커져서 유의수준 0.05의 기각역에 존재해서,
유의 확률인 p 값이 0.05보다 작아진다면
평균의 차이가 유의미하게 있다고 해석 되어
귀무가설을 기각한다.
그 반대의 경우,
평균의 차이가 유의미하지 않다고 해석 되어
귀무가설을 수용한다.
단측검정
특정 방향으로의 차이를 검정하고자 할 때 사용한다.
예시) 특정 약의 효과가 기존의 약보다 더 크다, 특정 처리 후 값이 증가/감소 할 것이다.
단측검정의 가설들
H0: 효과가 없거나, 차이가 없다. (Xa >= Xb or Xa <= Xb)
H1: 특정 방향으로 차이가 있다. (Xa < Xb or Xa > Xb)
즉, 검정은 특정 방향으로만 수행되며, 데이터가 기대되는 방향과 일치하는 경우에만 귀무가설을 기각할 수 있다.
양측 검정
차이가 어느 방향이든 있는지를 확인.
예시) 새로운 약이 기존보다 효과가 더 크거나 작을 수 있다.
H0: 차이가 없다, 둘이 같다. (Xa = Xb)
H1: 차이가 있다, 둘이 다르다. (Xa != Xb)
즉, 검정은 양방향으로 이루어지며 데이터가 어느쪽으로든 귀무가설과 일치하지 않으면, 귀무가설을 기각할 수 있다.
단측검정의 유의 수준이 양측검정에 비해 2배 크기 때문에, 양측검저이 더 엄격하다고 할 수 있다.
단측검정은 가설이 특정 방향으로 명확하게 제시될 때 적합하며,
양측검정은 차이가 어느 방향으로 나타날 수 잇는 경우에 사용된다.
T검정의 종류

우선 간단히,
독립 표본으로부터 추출된 연속형 자료가 정규성을 만족하면서,
동일한 분산일 때에는 스튜던트 T 검정 (Student's T Test)를,
동일한 집단의 약먹기 전, 후 혹은 한 그룹의 다이어트 전, 후 등을 대응표본 T 검정으로 확인할 수 있으며,
대응 표본으로부터 추출된 연속형 자료가 정규성을 만족할 때에는
동일 집단이므로 분산은 동일하니, 대응 표본 T 검정 (Paired T Test)을 실시한다.
이를 파이썬을 활용하면 다음과 같다.
정규성 검정
from scipy.stats import shapiro
normal1 = shapiro(x1)
normal2 = shapiro(x2)
print(normal1, normal2)
[output] (0.92, 0.37) (0.88, 0.14)
위의 경우 p값이 0.05보다 크기때문에, x1과 x2 모두 정규성을 띈다고 할 수 있다.
등분산성 확인
from scipy.stats import f
import numpy as np
df1, df2 = len(x1) - 1,len(x2) - 1
v = (np.var(x1, ddof=1), np.var(x2, ddof=1))
F = max(v) / min(v)
cdf = f(df1, df2).cdf(F)
p_value = 2 * min(cdf, 1 - cdf)
print(F, p_value)
[output] 1.25 0.74
위의 경우 p값이 0.05보다 크므로, 등분산성을 가진다고 할 수 있다.
더 간단히, Levene test와 Bartlett test 로도 확인할 수 있다.
from scipy.stats import levene, bartlett
levene(x1, x2)
[output] LeveneResult(statistic=0.0003, pvalue=0.98)
bartlett(x1, x2)
[output] BartlettResult(statistic=0.106, pvalue=0.74)
두 테스트 모두 p값이 0.05보다 크게 나왔으니, x1과 x2는 등분산성을 가진다고 할 수 있다.
일표본 T검정 One-Sample T Test
import scipy.stats as stats
import numpy as np
rand_samp = np.random.randn(1000) + 3
t_stat, p_val = stats.ttest_1samp(rand_samp, 3)
[output] 1.233, 0.216
numpy의 난수 생성으로 만들어진 rand_samp의
평균값이 3과 같을 것이다,
평균값이 3과 다를 것이다를
일표본 T검정을 통해 위와같이 알 수 있다.
위와같이 p값이 나온다면, 평균값이 3이다 라는 H0를 기각할 수 없다.
이 때, 대립가설을 3보다 크다 혹은 작다로 설정해 검정할 수도 있다.
t_stat, p_val = stats.ttest_1samp(rand_samp, 3, alternative="greater")
# alternative = "less" 로 해도 가능
이표본 T검정 Two-Sample T Test
import scipy.stats as stats
import numpy as np
rand_samp2 = 4.0 * np.random.randn(800) - 2.0
t_stat, p_val = stats.ttest_ind(rand_samp, rand_samp2, equal_var=True, alternative = "two-sided")
# two-sided를 통해 양측검정 수행
# equal_var를 통해 동분산성 확인, 분산이 다르다면 False
[output] 36.584, 1.854
####
t_stat, p_val = stats.ttest_ind(rand_samp, rand_samp2 +1 , equal_var=True, alternative = "two-sided")
위를 통해 rand_samp 와 rand_samp2의 평균이 같은지에 대한 검증을 수행할 수 있다.
즉, 귀무가설은 "두 샘플의 평균이 같다."가 되고, 대립가설은 "두 샘플의 평균은 다르다."가 된다.
위와 같이 p 값이 나온다면, "두 샘플의 평균이 같다."라는 귀무가설을 기각할 수 없다.
또한 아래처럼 샘플에 "+1"을 해주면 드 그룹의 평균의 차이가 특정 상수만큼 차이가 나는지를 검증할 수 있다.
즉, 귀무가설은 "두 샘플의 평균의 차가 1이다."가 되고, 대립가설은 "두 샘플의 평균의 차가 1이 아니다."가 된다.
대응표본 T검정 Paired Two-Sample T Test
from scipy.stats import ttest_rel
import numpy as np
rand_samp3 = np.random,randn(1000)
t_stat, p_val = ttest_rel(rand_samp, rand_samp3+3, alternative = 'less')
[output] 4.86, 0.0009
위의 경우 p값이 0.05보다 작으므로
두 그룹의 평균은 같다 라는 귀무가설을 기각하고,
두 그룹의 평균의 차는 통계적으로 유의하다고 말할 수 있다.
Frequentist vs Bayesian T-Test
T Test는 전통적으로 빈도론적 (Frequentist) 가설 검정 방법이고, 이표본 가설검정을 AB Test에 적용할 수도 있다.
AB Test의 주체가 연속형이라면 T Test를 수행할 수 있다.
BEST Bayesian Estimation Supersedes t-test
BEST 는 T-test에 베이지안 확률을 적용해서 고안한 확장된 t test이다.
둘의 차이점은 크게 다음과 같다.
| Frequentist | Bayesian | |
| 이상치가 포함되어도 괜찮은가? | No | Yes |
| 가설검정을 어떻게 하는가? | P-value 기반 | HDI 기반 |
먼저 Frequentist t-test는 A와 B방법에 노출된 두 데이터가 정규분포를 따른다고 가정하고,
표본 평균과 표본 분산을 통해 t 통계값을 계산하지만,
Bayesian의 경우 데이터가 T 분포를 따른다고 가정한다.
여기서 T 분포는 정규분포에 비해 꼬리의 두께가 두껍고, 그만큼 데이터의 분산이 더 크다고할 수 있으며,
그렇기에 이상치를 더 많이 포함한다고 할 수 있다.
BEST는 이상치가 있어도 분포 가정을 위배하지 않기 때문에 가설 검정 결과를 신뢰할 수 있다.
또, Frequentist t-test가 p-value를 활용해 검정을 한다는 것은,
귀무가설이 맞다는 전제 하에 표본에서 실제로 관측된 통계치와
같거나 더 극단적인 값이 관측될 확률이 0.05보다 적어야 함을 뜻한다.
하지만 이 p-value는 표본의 크기에 따라 바뀌는 문제가 있는데,
표본의 크기가 커지면 p-value는 작아져 가설을 기각하게 되는 경우가 생긴다.
https://boxnwhis.kr/2016/04/15/dont_be_overwhelmed_by_pvalue.html
A/B 테스트에서 p-value에 휘둘리지 않기
A/B 테스트에서 p-value에만 과하게 집중하는 것이 왜 좋지 않은지 설명합니다.
boxnwhis.kr
하지만 BEST의 경우, p-value를 대신해 HDI (Highest Densiti Interval)을 활용하기 때문에,
검정에 있어 분포에서 가장 높은 확률 밀도를 나타내는 범위를 확인하고,
이 범위 안에 있는 값들을 가장 신뢰할 수 있는 (Credible) 값들이라고 산정한다.
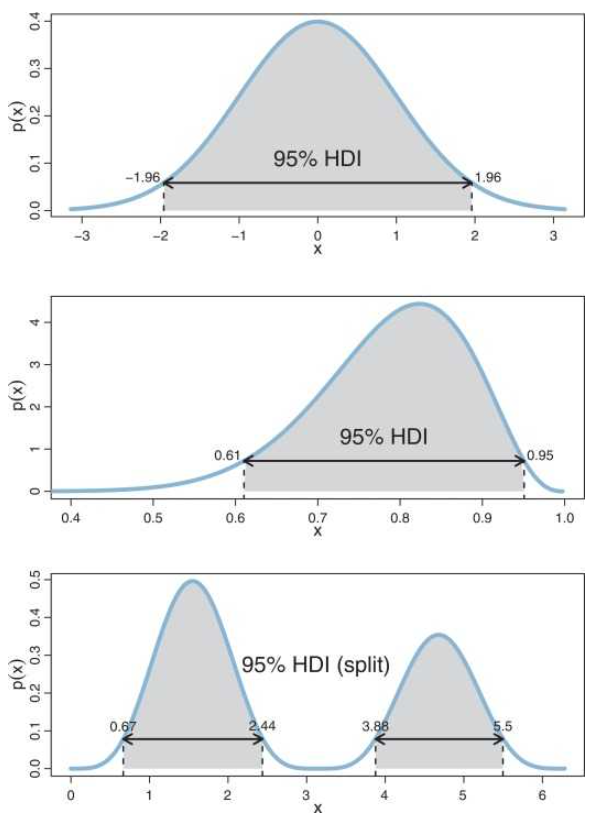
이는 신뢰구간 (Confidence Interval)과 비슷하지만,
"95%의 확률로 모수가 이 구간 안에 있다."
라는 뜻을 내포한다.
이는 "무한히 표본을 추출할 때마다, 표본의 평균은 95% 이 구간 안에 있다."라는 Frequentist의
이론적이고 가상적인 신뢰구간의 정의보다 더 직관적이며,
HDI가 0을 포함하는 구간이라면 귀무가설을 지지하고,
그렇지 않다면 대립가설을 지지하게 된다.
이를 파이썬을 활용해 분석하면 다음과 같다.
1) 각각 250명 씩 A 디자인과 B 디자인에 노출되었다.
2) A 디자인의 웹사이트의 평균 이용시간은 30이고 표준편차가 4인 정규분포를 따른다.
3) B 디자인의 웹사이트의 평균 이용시간은 26이고 표준편차가 7인 정규분포를 따른다.
import numpy as np
import matplotlib.pyplot as plt
import pymc as pm
N=250
mu_A, std_A = 30,4
mu_B, std_B = 26,7
duration_A = np.random.normal(mu_A,std_A,size=N)
duration_B = np.random.normal(mu_B,std_B,size=N)
print (duration_B[:8])
또, 베이지안의 BEST 모델에서는 데이터가 따르는 t 분포의
평균, 표준편차, 자유도가 다음과 같은 사전분포를 따른다고 가정한다.
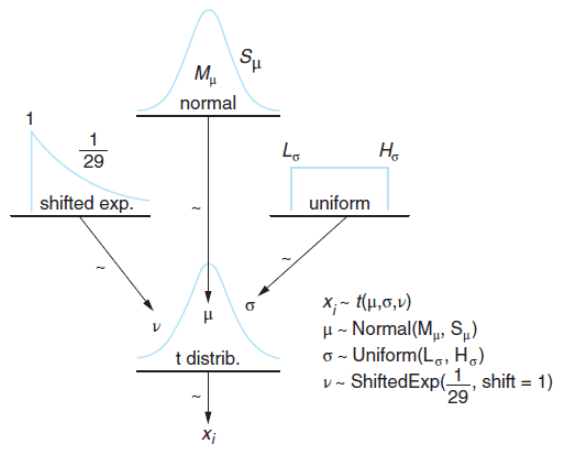
사전 분포
, μB 의 사전 분포: 정규 분포 (Normal Distribution)
- 평균: A 이용 시간과 B 이용 시간의 합동 평균 (pooled mean)
- 표준 편차: A 이용 시간과 B 이용 시간의 합동 표준 편차 (pooled standard deviation)$\times$1000
pooled_mean = np.r_[duration_A,duration_B].mean()
pooled_std = np.r_[duration_A,duration_B].std()
tau = 1/(1000*pooled_std**2) # precision parameter
# Prior on mu_A and mu_B
mu_A = pm.Normal("mu_A",pooled_mean,tau)
mu_B = pm.Normal("mu_B",pooled_mean,tau)
np.r_을 통해 duration_A와 duration_B를 한 array로 만들어 합동 평균과 합동 표준편차를 구한다.
tau는 정밀도 모수 (precision parameter)로, 1/분산 으로 정의된다,
pymc에서 Normal에 들어가는 모수가 평균과 정밀도이기에 필요한 값이다.
또한, , μB
σA, σB 의 사전 분포: 균등 분포 (Uniform Distribution)
- 하한 (Lower bound): 합동 표준 편차/1000
- 상한 (Upper bound): 합동 표준 편차*1000
std_A = pm.Uniform("std_A", pooled_std/1000, 1000*pooled_std)
std_B = pm.Uniform("std_B", pooled_std/1000, 1000*pooled_std)
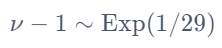
nu_minus_1 = pm.Exponential("nu-1",1/29)
이 때, 자유도는 항상 1 이상이니 이동된 지수 분포를 이요해서 최소값이 0이 아닌 1이 되도록 지정한다.
가능도
비중심 t-분포 (Noncentral t-distribution)
가능도는 t 분포를 사용하지만 자유도 v만 고려하면 되는 t 분포와는 다르게,
비중심 t 분포의 경우 자유도 v 외에도 Location Parameter "Mu"와 Scale 모수 "Lambda"를 가진다.
이 때의 Probability Density Function, PDF는 다음과 같다.
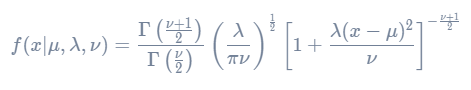
obs_A = pm.NoncentralT("obs_A",mu_A, 1/std_A**2, nu_minus_1+1, observed=True, value = duration_A)
obs_B = pm.NoncentralT("obs_B",mu_B, 1/std_B**2, nu_minus_1+1, observed=True, value = duration_B)
위 코드를 통해 duration_A와 duration_B가 비중심 t 분포를 따름을 보일 수 있다.
사후분포
Markov Chain Monte Carlo, MCMC Diagnostics
위의 사전분포와 가능도를 통해 MCMC Sample을 만들면 다음과 같다.
mcmc = pm.MCMC([obs_A,obs_B,mu_A,mu_B,std_A,std_B,nu_minus_1])
mcmc.sample(iter=25000,burn=10000)
mu_A_trace = mcmc.trace("mu_A")[:]
mu_B_trace = mcmc.trace("mu_B")[:]
std_A_trace = mcmc.trace("std_A")[:]
std_B_trace = mcmc.trace("std_B")[:] #[:]: trace object => ndarray
nu_trace = mcmc.trace("nu-1")[:]+1
sample()의 인자는 iter, burn, thin으로
iter는 전체 MCMC를 돌리는 횟수,
burn은 MCMC 초기 sample 중 버리는 갯수,
thin은 MCMC sample을 추출하는 간격을 의미다.
만약 iter=a, burn=b, thin=c로 설정되어 있다면, 최종적으로 갖게되는 사후 분포 sample의 개수는 (a-b)/c 이다
.
이제각 모수들의 사후 분포 Sample을 히스토그램으로 그리면 다음과 같다.
def _hist(data,label,**kwargs):
return plt.hist(data,bins=40,histtype="stepfilled",alpha=.95,label=label, **kwargs)
ax = plt.subplot(3,1,1)
_hist(mu_A_trace,"A")
_hist(mu_B_trace,"B")
plt.legend ()
plt.title("Posterior distributions of $\mu$")
ax=plt.subplot (3,1,2)
_hist(std_A_trace,"A")
_hist(std_B_trace,"B")
plt.legend ()
plt.title("Posterior distributions of $\sigma$")
ax=plt.subplot (3,1,3)
_hist(nu_trace,"",color="#7A68A6")
plt.title(r"Posterior distributions of $\nu$")
plt.xlabel("Value")
plt.ylabel("Density")
plt.tight_layout()
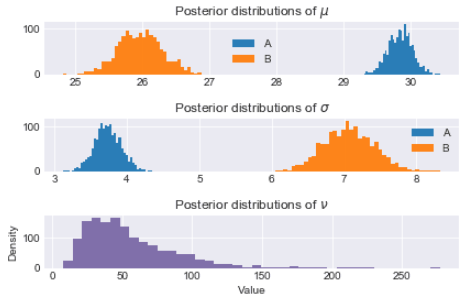
A의 이용시간이 B보다 후러씬 높음을 알 수 있고,
기존 세팅값 mu_A=30, mu_B=26와 거의 비슷하게 추정함을 확인할 수 있다.
이 때, mcmc.summary()를 통해 더 자세한 모수들의 값을 볼 수 있다.
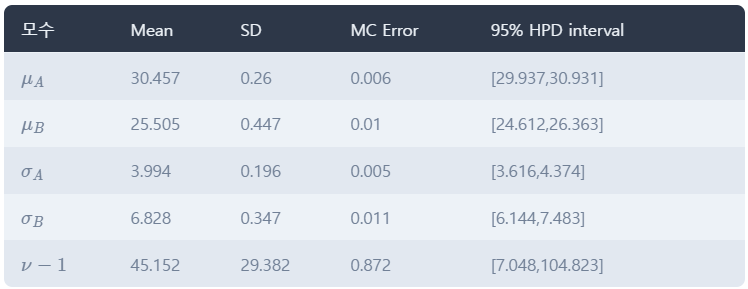
HPD 인터벌을 보면 실제 값인 μA=30,μB=26,σA=4,σB=7
MCMC sample이 잘 생성되었는 지 진단하는 방법은 pymc에 내장된 plot을 사용하면 된다.
pm.Matplot.plot(mcmc)
본 게시물은 다음 블로그 글을 기반으로 작성되었습니다.
https://playinpap.github.io/bayesian-abtest/
베이지안 A/B 테스트 in Python
베이지안 관점에서 AB Test를 하는 방법에 대해 정리했습니다. 전체 코드는 여기 에서 확인할 수 …
playinpap.github.io
'Statistics' 카테고리의 다른 글
| [STAT 101] 자유도와 카이제곱 분포, 검정 (1) | 2024.08.14 |
|---|---|
| [STAT 101] ANOVA 검정과 다중 검정의 문제 (0) | 2024.08.13 |
| [STAT 101] 베이지안 AB Test의 전환율 검정과 기대수익 분석 (4) | 2024.08.13 |
| [STAT 101] 베르누이 분포와 이항 분포, 그리고 포아송 분포 (0) | 2024.08.12 |
| [STAT 101] 정규분포(Normal Distribution)와 t분포(Student's t-distribution) (0) | 2024.08.09 |