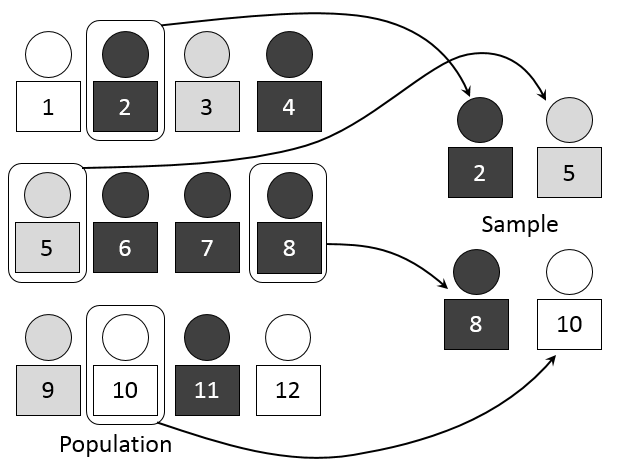
1. 모집단 Population
모집단은 관심의 대상이 되는 전체 집단을 의미한다.
예컨대, "대한민국 여성과 남성의 평균 키 차이"를 구하고 싶다면,
조사해야 하는 모집단은 "대한민국의 모든 여성과 남성"이 된다.
그러므로 모집단의 크기는 매우 클수도, 심지어 무한할수도 있고,
그래서 일반적으로 모집단의 모든 구성원에 대한 데이터를 수집하는 것은
불가능하거나 금전적, 시간적 제약이 크다.
# 모집단의 특성 (평균, 비율, 표준편차 등등)은 모수 (Parameter)라고 한다.
2. 표본 Sample
표본은 모집단의 일부로써 모집단을 대표할 수 있는 작은 그룹을 뜻한다.
모집단 전체를 알아보기에는 제약이 크니,
허용할 수 있는 오차/신뢰도를 만족하는 최소한의 표본을 추출하고 활용해서
모집단의 특성을 추정하는 것
하지만 표본은 "모집단의 일부"라는 한계가 있기에, 표본의 특성이 모집단의 특성을 100% 대변하지는 않는다.
그럼에도 그 수치를 99%, 혹은 99% 이상으로 늘릴수는 있으며,
이 때는 아래와 같은 사항을 고려해야 한다.
A. 추출할 표본집단의 크기 Sample Size
표본 수는 실행하고자 하는 분석의 목적, 방법, 그리고 원하는 분석 결과의 오차/신뢰도에 따라 다르게 계산되어야 한다.
만약 표본이 너무 작다면, 특이치와 예외적인 사람들을 불균형적으로 포함할 수 있다.
이렇게되면 결과가 왜곡되고 모집단을 제대로 대표할 수 없다.
만약 표본이 너무 크다면, 연구가 복잡해지고 비용과 시간적 제약이 증가한다.
애초에 표본을 추출하는 이유가 이런 것들을 줄이기 위함이었는데, 의미가 없어진다.
표본집단의 크기를 정할 때는 아래와 같은 변수들을 고려해야 한다.
1. 모집단 크기
총 몇명을 대상으로 하는지를 알아야 한다.
정확한 수치를 모를수도 있지만, 흔히 예상범위로 남기기도 한다.
2. 표본오차 (Sampling Error)와 오차범위 (허용오차, Margin of Error)
표본을 추출할 때 오차는 불가피하게 발생하며, 관건은 오차를 어느정도 허용하느냐다.
표본의 평균값과 모집단의 평균값 사이에서 어느정도로 오차를 허용할지 설정하는 것.
예시로는 다음과 같은 문구가 있다.
"고등학생 1000명의 평균 키는 170 cm이며, 오차범위는 +- 5cm 입니다."
이는 표본에서 계산된 값이 실제 모집단에서의 값의 ±5 cm 내에 있다는 뜻이다.
아래와 같이 표본오차 계산기도 사용해볼 수 있다.
https://www.omnicalculator.com/statistics/sampling-error
Sampling Error Calculator
Use this tool to calculate the sampling error incurred when inferring from a population.
www.omnicalculator.com
3. 신뢰구간 (Confidence Interval)
위와 같은 오차범위가 있다고 하면,
아래와 같이 신뢰구간을 통해 표현할 수도 있다.
"고등학생 1000명의 평균 키는 170 cm이며, 신뢰구간은 165 ~ 175cm 입니다."
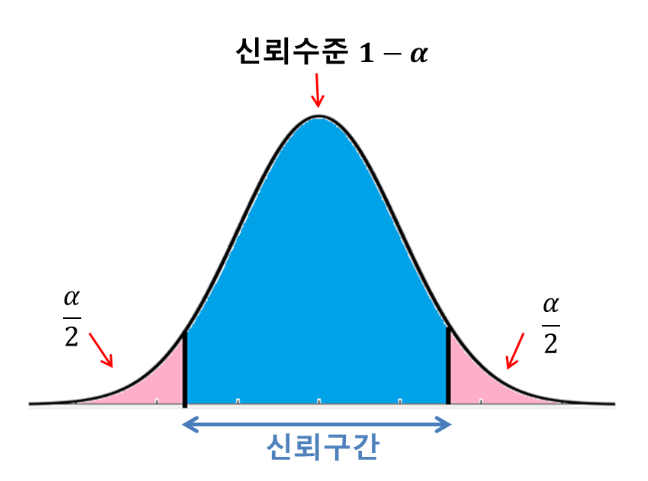
4. 신뢰도 (신뢰수준, Confidence Level)
신뢰구간과는 다르게, 신뢰도는 실제 평균이 신뢰구간 내에 위치할 확신의 정도를 뜻한다.

예를들어, 신뢰도가 95%라고 하면 동일한 방법으로 여러번 조사를 했을 때,
실제 모집단의 평균값이 계산된 오차범위 안에 포함될 확률이 95%라는 의미.
가장 일반적으로는 90%, 95%, 99%의 신뢰도가 주로 쓰인다.
" 고등학생 1000명의 평균 키는 170 cm이며, 오차범위는 +- 5cm, 신뢰도는 95%라면,
모든 표본들의 평균이 모평균 +- 5cm 사이에 존재할 확률은 95%가 되는 것 "
5. 표준 편차 (Standard Deviation, SD)
샘플의 값들이 서로 얼마나 상이하고 평균과 차이가 나는지 측정하는 지표.
표준 편차가 낮을수록 서로 평균값 근처에 분포하게 된다.
" 표준편차: 제곱근(분산 = 편차 제곱의 평균) "
| 표준편차 크기 | 판단 기준 |
| 0 ~ 1 | 매우 작음 |
| 1 ~ 2 | 작음 |
| 2 ~ 3 | 보통 |
| 3 ~ 4 | 큼 |
| 4 이상 | 매우 큼 |
6. 표준오차 (Standard Error of Sample Mean, SE)
" 표본 평균 추정값의 변동성 "
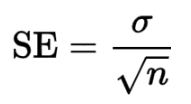
표준편차를 표본크기의 제곱근으로 나눈 값으로,
표본들의 평균이 모평균과 얼마나 떨어져있는지? 를 알려준다.

신뢰도, 신뢰구간 (오차범위), 집단의 수를 알고있다면
간단하게 아래의 표본 크기 계산기를 통해 적절한 표본 크기를 알아볼 수 있다.
https://www.qualtrics.com/blog/calculating-sample-size/
Sample Size Calculator - Qualtrics
Need to quickly calculate sample size? Use our calculator to find your ideal sample size now! ✓ Learn more with this complete guide.
www.qualtrics.com
B. 표본 추출 방법 Sampling Method
1. 단순 무작위 추출 Simple Random Sampling
예시: 복권 추첨, 무작위 난수 표본 추출
장점: 가장 간단하고 이해하기 쉬운 방법, 표본 오류가 가장 적음
단점: 모집단의 목록을 다 작성해야하기에 어렵거나 시간이 많이 소요될 수 있음.
그래서 대규모 모집단에서는 사용 못 할수도 있음
2. 계통 무작위 추출 Systematic Random Sampling
모집단을 일정한 간격으로 나열하고, 시작점을 난수로 선택해 그 간격으로 표본을 선택하는 방법.
예시: 설문조사 대상자를 일정한 간격으로 선정
장점: 단순 무작위 표본 추출보다 추출 과정이 간단하고 대규모 모집단에도 적용 가능.
단점: 모집단이 일정한 간격으로 분포되어 있지 않으면 표본 오류 발생 가능
3. 층화 무작위 추출 Stratified Random Sampling
모집단을 특정 기준으로 층을 나누고, 각 층에서 무작위 표본을 선택하는 방법.
하지만 층을 나누는 기준에 따라 표본 오류가 발생할 수 있음.
예시: 성별, 연령, 지역별로 층화해 표본 추출
장점: 모집단의 특성을 잘 반영하는 표본을 얻을 수 있음. 표본 오류를 줄일 수 있음.
단점: 층을 나누는 기준에 따라 표본 오류가 발생할 수 있음. 층화 과정이 복잡하고 시간이 많이 소요될 수 있음.
4. 군집 무작위 추출 Cluster Random Sampling
모집단을 군집으로 나누고, 무작위로 군집을 선택한 후 그 군집에 속한 모든 대상을 표본으로 선택하는 방법.
예시: 학교를 군집으로 나누고, 무작위로 학교를 선택해 학생들을 표본으로 선택
장점: 대규모 모집단에 적용하기 용이함. 표본 추출 과정이 비교적 간단함.
단점: 군집 내의 대상들이 서로 유사할 경우, 표본 오류가 발생할 수 있음.
'Statistics' 카테고리의 다른 글
| [STAT 101] 베르누이 분포와 이항 분포, 그리고 포아송 분포 (0) | 2024.08.12 |
|---|---|
| [STAT 101] 정규분포(Normal Distribution)와 t분포(Student's t-distribution) (0) | 2024.08.09 |
| [STAT 101] 잔차와 오차, 그리고 결정계수 (0) | 2024.07.16 |
| [STAT 101] 단순선형회귀, 공분산과 상관관계 (0) | 2024.07.04 |
| [STAT 101] T - Test (0) | 2024.07.04 |