1. 단순선형회귀
단순 선형 회귀는 두 변수 사이의 관계를 모델링하는 통계기법이다.
이 때, 하나는 독립 변수 X (설명 변수), 나머지 하나는 종속 변수 Y (반응 변수)로 하며, 선형 회귀는 둘 사이의 선형관계를 찾는다.

Beta-0는 Y 절편 (Y-intercept)
Beta-1은 기울기 (Slope)
ϵ은 오차 항(Error Term), 혹은 확률변동 (Random Disturbance) 라고 한다.
ㄴ 실제 자료와 참회귀선 (y = beta0 + beta1 x) 의 차이를 나타낸다.
최소 제곱법
위는 최소 제곱법 (Least Square Method)을 활용해서
각 점으로부터 구하고자 하는 최적의 직선까지의 수직거리의 제곱합을 최소로 하는 직선
방정식을 구한다. 이는 RMSE (Root-mean Square Error)를 최소화하는 방식이다.
RMSE는 회귀의 표준오차로, 실제 값과 예측치의 차이가 어느정도 될지 알려주는 수치이다.


최소 제곱법을 활용하면 Beta-0 와 Beta-1은 아래와 같다.

앞서 설명한 것들을 아래와 같은 예시 파이썬 코드로 수행할 수 있다.
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Example data
X = np.array([1, 2, 3, 4, 5]).reshape(-1, 1) # Independent variable
Y = np.array([2, 3, 5, 6, 8]) # Dependent variable
# Create and train the model
model = LinearRegression()
model.fit(X, Y)
# Regression coefficients
beta_1 = model.coef_[0]
beta_0 = model.intercept_
print(f"Slope (β1): {beta_1}")
print(f"Intercept (β0): {beta_0}")
# Predicted values
Y_pred = model.predict(X)
# Visualization
plt.scatter(X, Y, color='blue', label='Actual data')
plt.plot(X, Y_pred, color='red', label='Regression line')
plt.xlabel('Independent variable (X)')
plt.ylabel('Dependent variable (Y)')
plt.legend()
plt.show()
2. 공분산과 상관계수
종속변수 Y와 독립변수 X로 구성된 n개의 레코드 중, Y와 X 간 연관관계의 방향과 강도를 구하는 지표들이다.
a. 공분산
두 변수 간의 관계의 방향을 나타낸다.

두 변수의 공분산을 나타내는 해당식이
0보다 크면 우상향의 양의 관계,
0보다 작으면 우하향의 음의 관계를 가진다.
해당 식은 -무한대 과 무한대 사이의 값을 가진다.
공분산이 0이면 두 변수는 선형 관계를 가지지 않음을 뜻한다.
공분산으로 방향성은 알 수 있지만,
공분산 값의 크기는 변수의 단위에 따라 달라지기 때문에,
두 변수 간의 관계 정도 자체는 해석하기 어려울 수 있다.
공분산은 아래와 같은 예시 파이썬 코드로 구할 수 있다.
import numpy as np
# Example data
X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 3, 5, 6, 8])
# Mean of X and Y
mean_X = np.mean(X)
mean_Y = np.mean(Y)
# Calculate covariance
covariance = np.mean((X - mean_X) * (Y - mean_Y))
print(f"Covariance: {covariance}")
b. 상관계수
상관계수는 공분산을 두 변수의 표준편차로 나눈 값으로, 두 변수의 단위에 독립적으로 관계 강도를 나타내기에 공분산 보다 해석에 용이하다.
표본평균을 x바, y바로, 표본표준편차를 SDx와 SDy로 나타낼 때,
두 변수 간의 상관계수는 다음과 같이 나타낼 수 있다.

해당 식의 분모 분자를 자유도 n-1로 나누면 아래와 같아진다.
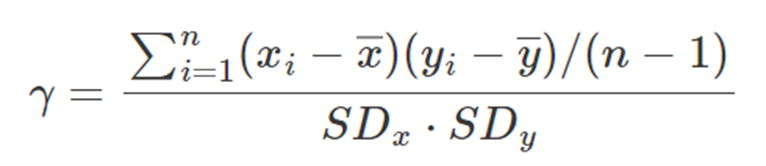
이는 다시 아래와 같아진다.
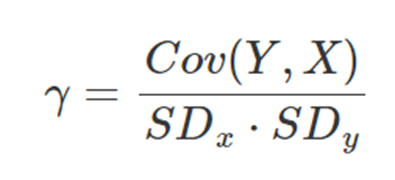
상관계수도 공분산과 같이 -1과 1 사이의 값을 가진다.
a. 상관계수 = 1 : 완전한 양의 선형 관계. 한 변수가 증가할 때, 다른 변수도 일정 비율로 증가한다.
b. 상관계수 = -1 : 완전한 음의 선형 관계. 한 변수가 증가할 때, 다른 변수는 일정 비율로 감소한다.
c. 상관계수 = 0 : 두 변수 간의 선형 관계가 없음을 의미. 두 변수는 독립적이거나 선형관계가 없음을 뜻함.
상관계수는 다음과 같은 예시 파이썬 코드로 구할 수 있다.
import numpy as np
# Example data
X = np.array([1, 2, 3, 4, 5])
Y = np.array([2, 3, 5, 6, 8])
# Calculate correlation coefficient
correlation_coefficient = np.corrcoef(X, Y)[0, 1]
print(f"Correlation Coefficient: {correlation_coefficient}")
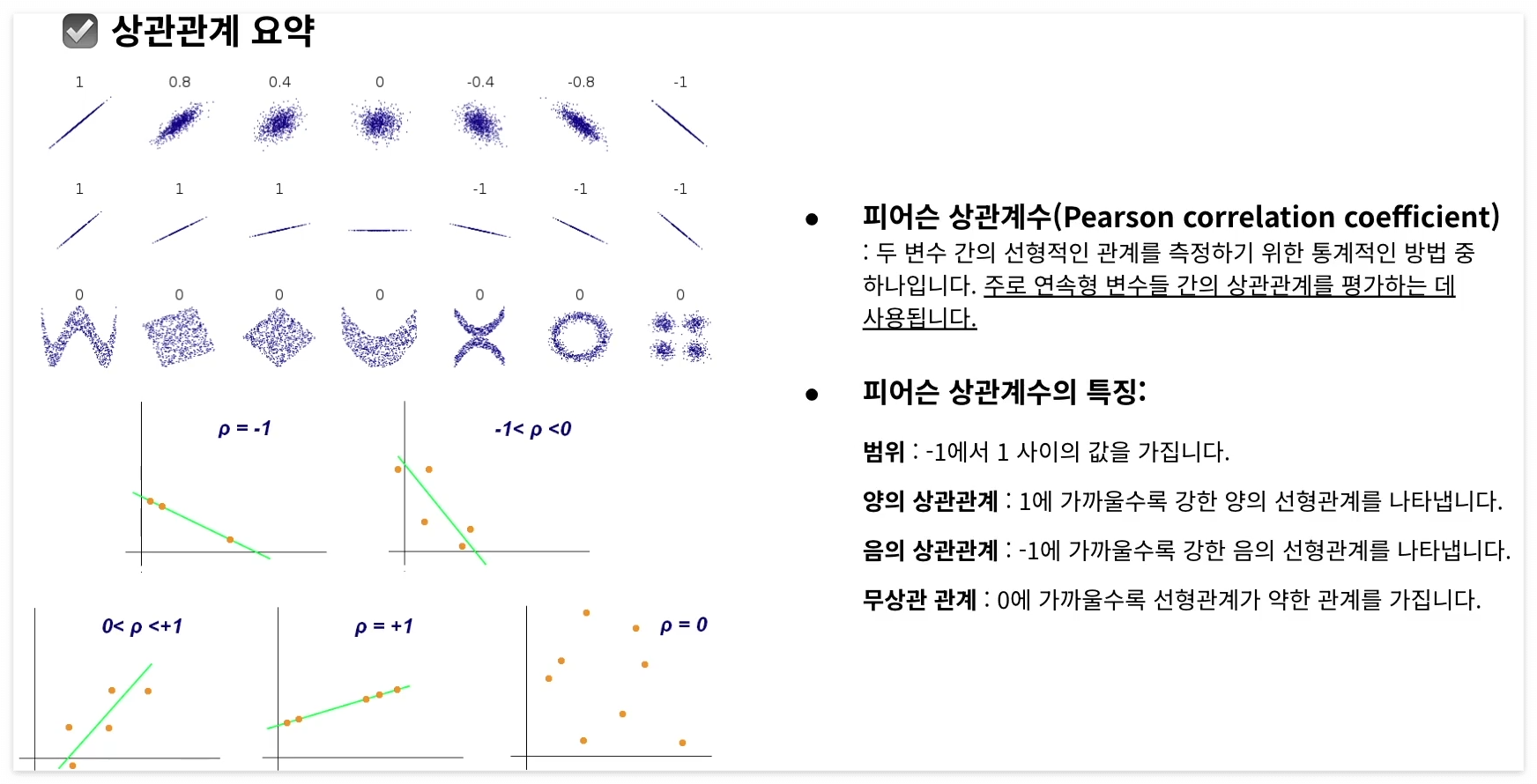
상관관계
예시) 피어슨 상관계수
'Statistics' 카테고리의 다른 글
| [STAT 101] 모집단과 표본, 그 속 통계 값들과 표본 추출 방법 (0) | 2024.08.07 |
|---|---|
| [STAT 101] 잔차와 오차, 그리고 결정계수 (0) | 2024.07.16 |
| [STAT 101] T - Test (0) | 2024.07.04 |
| [STAT 101] 가설과 가설 검정 (0) | 2024.07.04 |
| [STAT 101] 정규화 (Normalization)와 표준화 (Standardization) (0) | 2024.07.04 |