오늘은 아래의 아티클을 읽고 이를 정리해보았다.
태블로 Tableau란? 기능 소개, 사용 방법, 가격 후기 - 뉴스젤리 : 데이터 시각화 전문 기업
데이터에 대한 생각을 바꾸는 Tableau
newsjel.ly
추가로, 태블로에 예측 기능이 있는 것을 알았고 이에 대해 리서치를 해보았다.
1. 많은 양의 데이터를 빠르게 연동하기
태블로는 파일, 서버에 연결하는 두 가지 방법으로 데이터를 업로드 할 수 있다.파일의 경우 엑셀, csv, pdf 등 여러 형태를 업로드할 수 있다.
2. 추천 시스템을 통한 쉬운 차트 시각화
드래그 앤 드롭 방식으로 손쉽게 시트를 시각화할 수 있다.데이터의 차원과 측정값을 동시에 선택해 우측 화면에 '표현 방식'을 보는 것으로 원하는 시각화를 할 수 있다.
3. 통계 기능을 통해 데이터 분석하기
'분석' 탭을 통해 시각화와 함께 데이터의 통계분석을 진행할 수 있다.요약, 모델, 사용자 지정을 통해 원하는 분석 방식을 지정할 수 있고, 나아가 '예측' 모델을 통해 실제와 예상값으로 나눠 앞으로의 수치를 확인할 수 있다.
4. 다양한 디바이스에서도 활용 가능
필요한 핵심 그래프만 조합한 데이터를 '대시보드'라고 하는데, 태블로는 드래그 앤 드랍 만으로 대시보드를 손쉽게 구성할 수 있다. 이를 Tableau Server 혹은 Tableau Online에 게시하는 것으로 손쉽게 공유할 수 있다.
Tableu는 드래그 앤 드랍 만으로 모든 기능을 활용할 수 있다 해도 과언이 아니라고 한다. 비록 다른 BI보다 배우는 데 더 시간이 소요될 수 있지만, 더욱 다양한 인사이트를 제공할 좋은 BI툴이라고 할 수 있다.
Tableau의 예측 프로세스
그렇다면 Tableau의 예측은 어떻게 진행되는 것일까?
태블로는 날짜 필드와 적어도 하나의 측정값을 포함하는 뷰에 예측이 가능하고, 날짜가 없더라도 정수값의 차원과 하나의 측정값을 포함한다면 예측값을 생성할 수 있다.
모든 예측 알고리즘은 기본적인 DGP (Data Generating Process, 데이터 생성 프로세스) 모델이며, 이 중 최상의 모델을 8개까지 자동으로 선택하고, 이 중 가장 높은 품질의 예측을 생성하는 모델을 선택한다. 이 때 사용되는 함수는 선형 회귀, 정규화 선형 회귀, 가우스 프로세스 회귀를 지원한다고 한다.
1. 선형 회귀, Linear Regression
태블로는 데이터의 변수들 사이의 관계를 파악하기 위해 선형 회귀를 사용한다. 이렇게 나온 직선식을 통해 독립변수마다 종속변수의 값을 예측한다.

선형회귀는 보통 위와 같은 식처럼 m (slope or weight, 기울기 혹은 가중치)과 b (절편, intercept)를 통해 x와 y의 관계를 설명하는 1차 방정식이 나온다.

여러 독립변수를 사용하는 다중 선형 회귀의 경우 위와 같은 수식이 활용되며, 이 경우, 사용된 독립변수마다 다른 w (가중치) 값을 가지게 된다.
2. 이동 평균, Moving Average
시계열 데이터에서 주로 사용되는 방법으로, 일정 기간 동안의 평균 값을 이용해 시계열 데이터의 추세를 부드럽게 (Smoothing) 한다. 단순 이동 평균, 가중 이동 평균 등을 통해 미래 값을 예측할 수 있다. 예컨대, 지난 몇 주간의 판매량의 평균을 바탕으로 앞으로의 판매량을 예측하는 것이다.
이동평균은 크게 다음과 같이 분류할 수 있다.
a. 단순 이동 평균, Simple Moving Average (SMA)
SMA는 일정한 기간 동안의 데이터 값을 평균내어 구하는 방법이다.

이 때의 수식은 위와 같으며, t 는 기준 시점 (i는 이전을 뜻한다.), n은 평균을 구하는 기간 (5일의 평균을 구하려면 n=5)이 된다.
이를 이용한 예측은 다음과 같으며,

현재의 이동 평균 값을 그대로 사용해 예측값으로 할 수 있다.
b. 가중 이동 평균, Weight Moving Average (WMA)
WMA는 데이터 포인트마다 다른 가중치를 활용해 이동 평균값을 구한다. 예컨대, 가장 최근 데이터는 3배, 그 전날은 2배, 그 이전은 1배, 아주 오래 전 데이터는 0.5배로 가중치를 주어 평균을 계산할 수 있다.

이 때의 수식은 위와 같으며 SMA와 다르게 가중치들의 합으로 가중치를 곱한 관측값 X의 합을 나눈다. t 는 기준 시점 (i는 이전을 뜻한다.), n은 평균을 구하는 기간, Wi는 (t - i) 시점에서의 가중치가 된다. 이 때, 일반적으로 가장 최근의 데이터에 더 높은 가중치를 준다.
예컨대, i = 0이라면 오늘, 1 이라면 하루 전을 뜻하게 되며, n = 5일 때 W0, W1, ... W4 까지의 가중치가 주어진다. 이 때, 가장 최근 데이터에 높은 가중치를 주고싶다면 W0 = 5로 하고, W4 = 1로 계산하면 된다.
이를 통해 SMA 보다 최근 트렌드를 더 반영할 수 있다.
3. 시계열 예측, Time Series Forecasting
시계열 예측에는 지수 평활법 (Exponential Smoothing) 같은 고급 방법이 사용되기도 한다. 이를 통해 데이터의 계절성과 트렌드를 기반해서 미래 값을 예측한다. 예컨대, 월 별 매출 데이터, 혹은 휴일 별 데이터를 활용해 분기 마다 다른 점을 파악하고, 이를 예측에 투영한다.
a. 지수 이동 평균 (Exponential Moving Average, EMA)
EMA 또한 이동 평균을 구하는 방법 중 하나지만, SMA와 WMA이 섞여있다. 예컨대, EMA는 SMA로 시작하지만 이후 각 데이터 포인트에 지수적으로 감소하는 가중치를 적용한다.

이 때, t 는 기준 시점, Xt는 시점 t에서의 관측값, EMA_(t - 1)은 이전 시점에서의 EMA 값이다.
한 가지 특이한 것은 α인데, 이는 0과 1 사이의 값을 가지는 평활 계수 (Smoothing Coefficient)이다. EMA의 반응성을 결정하는 평활 계수는 아래와 같이 구할 수 있으며,
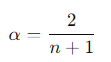
이 때 n은 EMA를 계산하는 기간이다. (즉 3일을 계산한다면 n = 3이 되며, α 값은 2 / (3+1)로 0.5가 된다.) α 값이 클 수록 최근 데이터에 더 많은 가중치를 주게 되며, EMA 데이터는 변화에 더 빠르게 반응한다. 반대로 α 값이 작을 수록 과거의 데이터를 더 많이 반영하고, 그래프가 더 부드러운 곡선을 그리게 된다.
EMA를 계산할 때는 EMA_(t - 1), 즉 이전 시전의 값이 필요하기 때문에 기준이 되는 초기 값이 필요하며, 이를 같은 t값을 가지는 SMA로 설정할 수 있다. (혹은 최초의 데이터로 대체한다.)
즉, n = 3일 때 EMA의 초기값은 아래와 같이, n = 3인 SMA의 값과 같다.
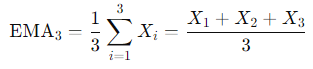
n = 3일 때의 α 값은 2 / (3+1)로 0.5가 되므로,
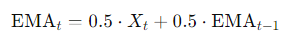
가 되고, 이를 활용해 EMA들을 구하면
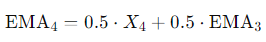
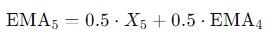
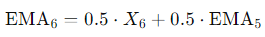
가 되며, 이를 기준시점 t 까지 구해주면 된다.
4. 예측 모델 구성
태블로에서는 추가로 분석 변수, 데이터 기간, 평활 수준 등을 조정할 수 있다. 즉 파라미터 튜닝이 가능하며, 이를 통해 예측 모델을 보다 정교하게 구성할 수 있다. 태블로는 이를 자동으로 해주기도 하며, 시각화까지 완료해주어 결과를 직관적으로 파악할 수 있게 도와준다.
5. 실무 적용
위에서 봤듯이, 평활법을 사용하면 데이터 포인트마다 가중치를 달리 해서 데이터를 평활화 할 수 있다.
선형회귀는 이렇게 평활화 된 데이터를 기반으로 더 정확한 추세를 알 수 있다. 이는 노이즈가 많은 데이터에서 유용할 수 있으며 이동평균을 사용해 데이터의 노이즈를 제거하고 선형회귀로 장기적인 추세를 예측하는 방식을 적용할 수 있다.
'오늘 나는 (TIL)' 카테고리의 다른 글
| [TIL 240906] 딥러닝 속 ANN (Artificial Neural Network)과 GA (Genetic Algorithm) (0) | 2024.09.06 |
|---|---|
| [TIL 240904] Pandas 데이터 프레임 변형 (Pivot, Stack and Melt 등등) (1) | 2024.09.04 |
| [TIL 240820] 머신러닝 10가지 알고리즘 (0) | 2024.08.20 |
| [TIL 240816] 데이터 분석가의 커뮤니케이션 (0) | 2024.08.16 |
| [TIL 240814] 분산분석 ANOVA 검정과 다중 검정의 문제 (0) | 2024.08.13 |